Floor Effect Vs Ceiling Effect Statistics

In layperson terms your questions are too hard for the group you are testing.

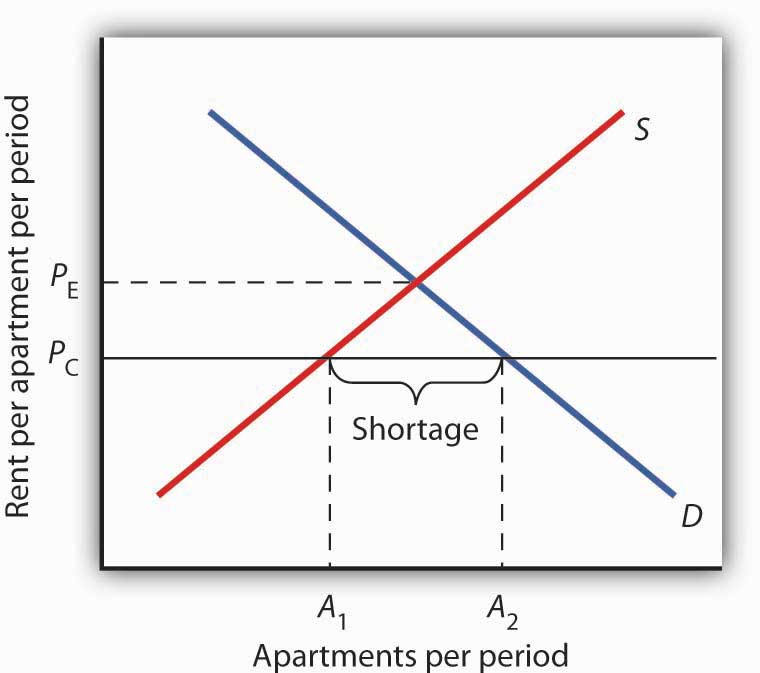
Floor effect vs ceiling effect statistics. The ceiling effect is one type of scale attenuation effect. Let s talk about floor and ceiling effects for a minute. Note that one of the groups was further offset with respect to c l on the horizontal axis which explains why the graphs are not fully symmetric around c l 0. The lower limit which affects dependent variables is referred to as the floor and can badly skew a data distribution if not accounted for.

How to detect ceiling and floor effects if the maximum or minimum value of a dependent variable is known then one can detect ceiling or floor effects easily. As c l decreases floor effect increases while as c l increases the ceiling effect increases in magnitude. This strongly suggests that the dependent variable should not be open ended. The other scale attenuation effect is the floor effect the ceiling effect is observed when an independent variable no longer has an effect on a dependent variable or the level above which variance in an independent variable is no longer measurable.

The specific application varies slightly in differentiating between two areas of use for this term. The other scale attenuation effect is the ceiling effect. In research a floor effect aka basement effect is when measurements of the dependent variable the variable exposed to the independent variable and then measured result in very low scores on the measurement scale. This could be hiding a possible effect of the independent variable the variable being manipulated.

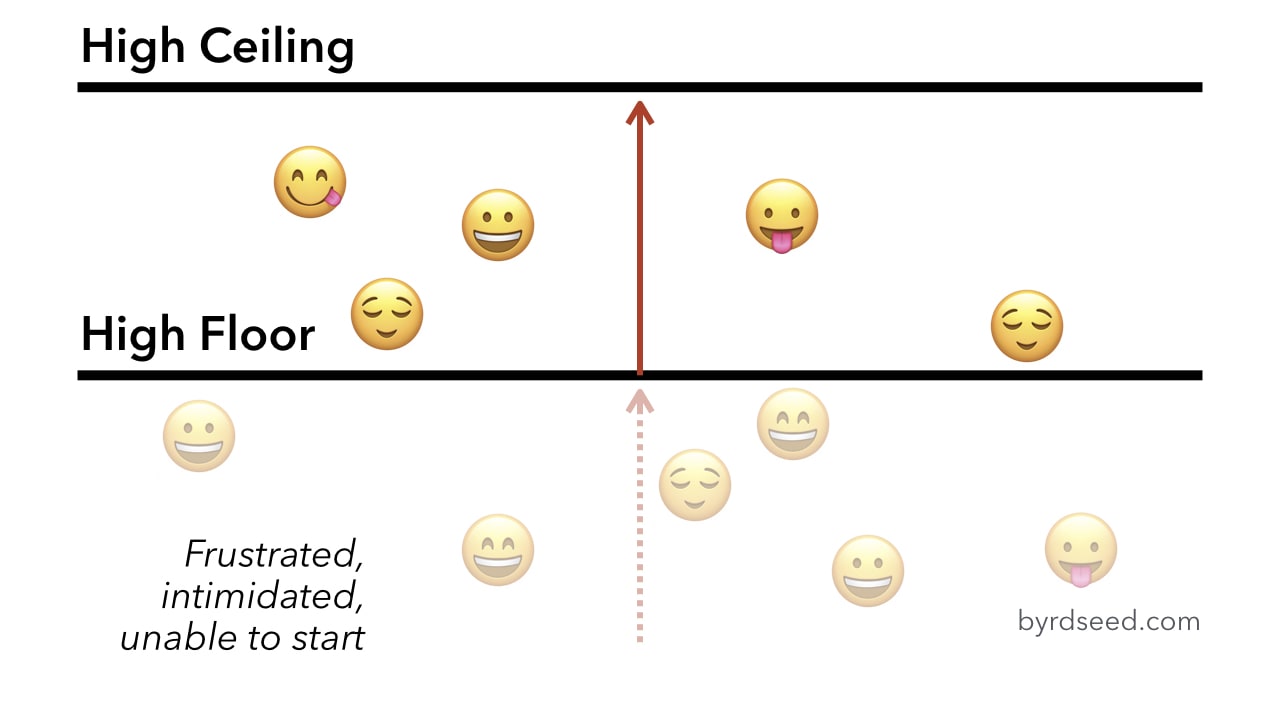
Usually this is because of inherent weaknesses in the measuring devices or the measurement scoring system. An example of use in the first area a ceiling effect. A floor effect is when most of your subjects score near the bottom. This lower limit is known as the floor.

The inability of a test to measure or discriminate below a certain point usually because its items are too difficult. This is even more of a problem with multiple choice tests. The floor effect is what happens when there is an artificial lower limit below which data levels can t be measured. In statistics a floor effect also known as a basement effect arises when a data gathering instrument has a lower limit to the data values it can reliably specify.

For example the distribution of scores on an ability test will be skewed by a floor effect if the test is much too difficult for many of the respondents and many of them obtain zero scores. For example it is easy to see a ceiling effect if y is a percentage score that approaches 100 in the. If the floor or ceiling effects cause your data to become dichotomous or can easily be collapsed into two categories without much loss of information and you want to predict that variable then.