Floor Function Limit Proof

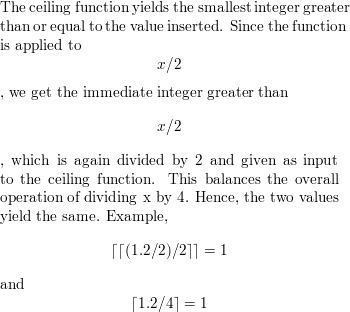
Floor and ceiling functions.

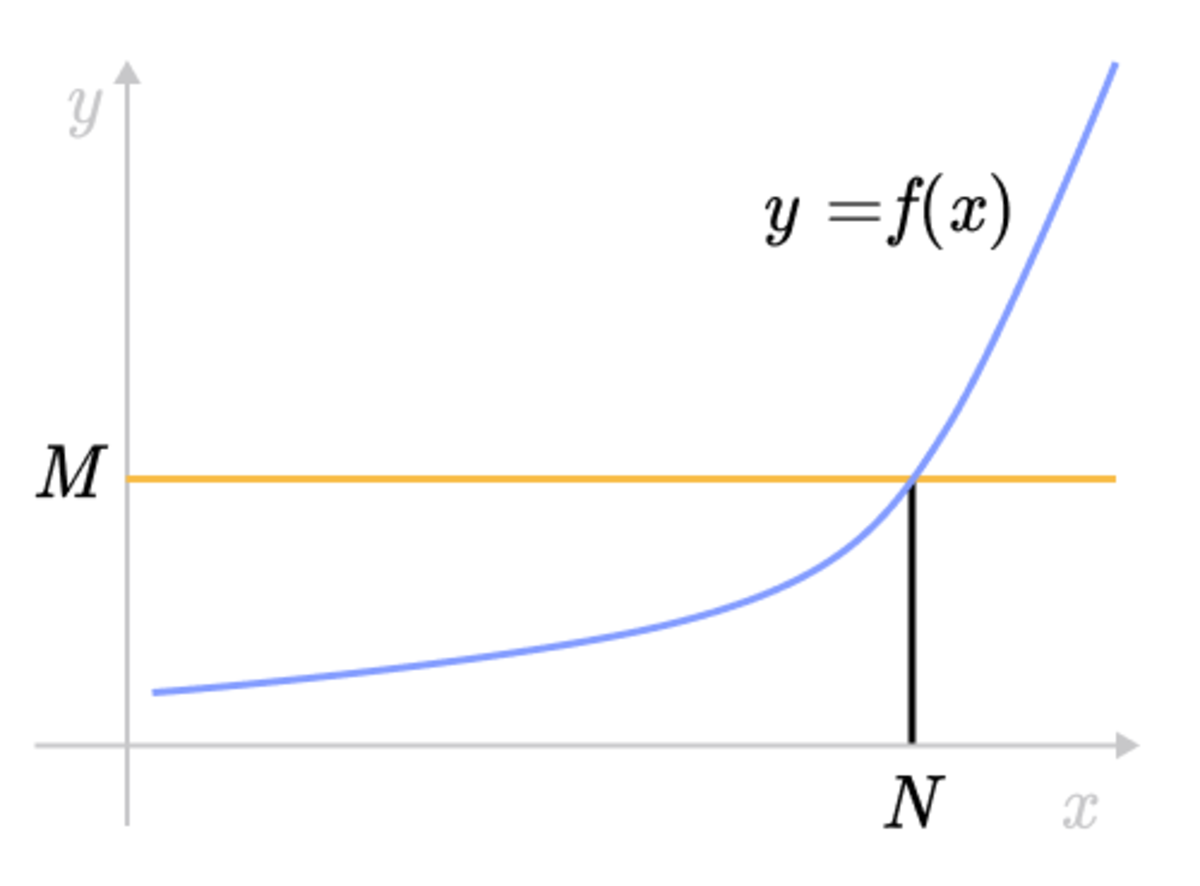
Floor function limit proof. We can take δ 1 n delta frac1n δ n 1 and the proof of the second statement is similar. For y fixed and x a multiple of y the fourier series given converges to y 2 rather than to x mod y 0. At points of continuity the series converges to the true. The graphs of these functions are shown below.

For example b3 7c 3 dπe 4 b5c 5 d5e b πc 4 d πe 3. Ceiling and floor functions. So the function increases without bound on the right side and decreases without bound on the left side. 0 x.

The best strategy is to break up the interval of integration or summation into pieces on which the floor function is constant. Int limits 0 infty lfloor x rfloor e x dx. Definite integrals and sums involving the floor function are quite common in problems and applications. The value of a.

Formal definition of a function limit. And this is the ceiling function. Some say int 3 65 4 the same as the floor function. Evaluate 0 x e x d x.

At points of discontinuity a fourier series converges to a value that is the average of its limits on the left and the right unlike the floor ceiling and fractional part functions.