Floor Function Of 1 5

Floor number significance the floor function syntax has the following arguments.

Floor function of 1 5. Floor 1 5 1 floor 0 0. Rounds number down toward zero to the nearest multiple of significance. The numeric value you want to round. Unfortunately in many older and current works e g honsberger 1976 p.

A solid dot means including and an open dot means not including. Select floor 123 45 floor 123 45 floor 123 45. Floor 1 6 equals 1 floor 1 2 equals 2 calculator. For example and while.

Example evaluate floor x for various values of x. The floor function also called the greatest integer function or integer value spanier and oldham 1987 gives the largest integer less than or equal to the name and symbol for the floor function were coined by k. An open dot at y 1 so it does not include x 2 and a solid dot at y 2 which does include x 2. In mathematics and computer science the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to denoted or similarly the ceiling function maps to the least integer greater than or equal to denoted or.

The floor function is this curious step function like an infinite staircase. At x 2 we meet. The following example shows positive numeric negative numeric and values with the floor function. This article describes the formula syntax and usage of the floor function in microsoft excel.

0 x. Definite integrals and sums involving the floor function are quite common in problems and applications. Floor x rounds the number x down examples. The floor function floor x is defined as the function that gives the highest integer less than or equal to x.

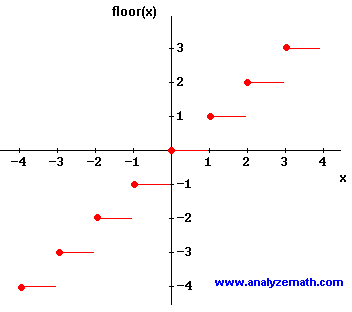
The graph of floor x is shown below. The domain of floor x is the set of all real numbers while the range of floor x is the set of all integers. The result is the integer part of the calculated value in the same data type as numeric expression. The best strategy is to break up the interval of integration or summation into pieces on which the floor function is constant.